概率论与数理统计

第一章 随机事件及其概率

样本点：对于随机试验，把每一个可能的结果称为样本点

随机事件：某些样本点的集合

基本事件：单个样本点构成的集合

样本空间(或必然事件)：所有样本点构成的集合，记作 Ω

不可能事件：不含任何样本点，记作 $\oslash$

事件关系运算

交换律：$A\cup B=B \cup A, ~~A\cap B=B \cap A$

结合律：$A\cup (B\cup C)=(A\cup B)\cup C, ~A(BC)=(AB)C$

分配律：$A(B\cup C)=(AB)\cup (AC)$, $(AB)\cup C=(A\cup C)(B\cup C)$, $A(B-C)=AB-AC$

对偶率：$\overline{A\cup B}=\overline{A}\cap \overline{B}$, $\overline{A\cap B}=\overline{A}\cup \overline{B}$

事件的积：$A\cap B=AB$

事件的和：$A\cup B\xrightarrow[直和]{AB互不相容}A+B$

事件的差：$A-B=A\Omega-AB=A\overline{B}$

概率性质

1. 对于任意事件A，$0 \le P(A)\le 1$

2. $P(Ω)=1， P(\oslash)=0$

3. 对于两两互斥的有限多个事件$A_1~, A_2~, ..., A_m~$

   $P(A_1~+A_2~+...+A_m~) = P(A_1~) + P(A_2~) + ... + P(A_m~)$

推论

1. $P(\overline A)=1-P(A)$

2. 任意时候：$P(A-B)=P(A)-P(AB)$

   若 $A\supset B$ , 则 $P(A-B)=P(A)-P(B)$

3. $P(A\cup B)=P(A)+P(B)-P(AB)$

   因此，$P(AB)=P(A)+P(B)-P(A\cup B)$

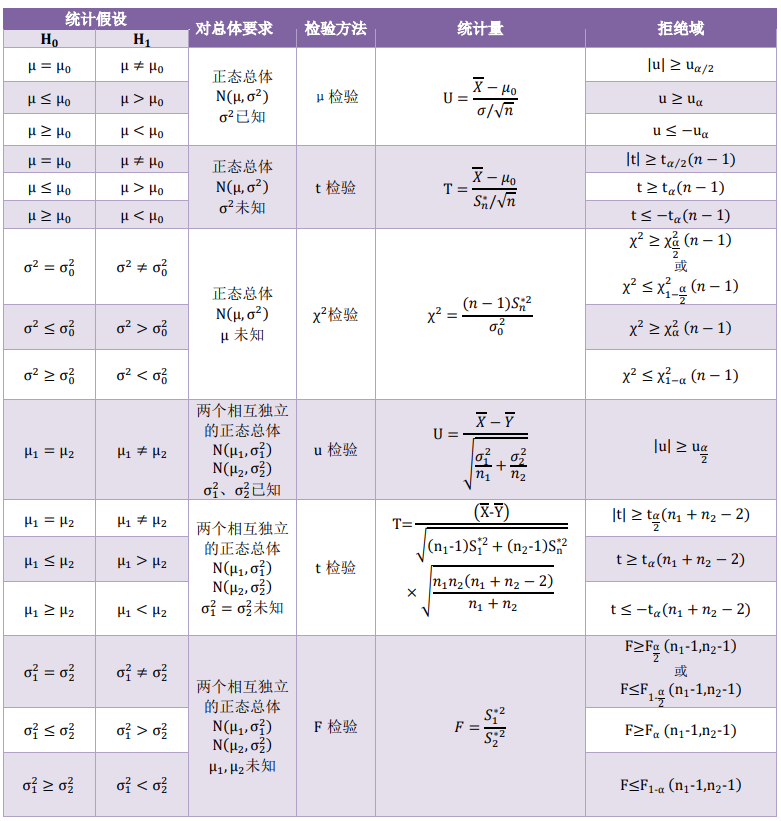
条件概率 全概率公式 Bayes公式

条件概率

$P(A|B)=\frac{P(AB)}{P(B)}$

乘法定理 $P(AB)=P(B)P(A|B)=P(A)P(B|A)$

全概率公式

$$P(B)=\sum_{i=1}^{n}P(A_i B)=\sum_{i=1}^{n}P(A_i)P(B|A_i)$$

Bayes公式

$$P(A_i|B)=\frac{P(A_iB)}{P(B)}=\frac{P(A_i)P(B|Ai)}{\sum_{i=1}^{n}P(A_i)P(B|A_i)}$$

事件的独立性

定义：若 $P(AB)=P(A)P(B)$, 则A与B是相互独立的

性质：

1. 必然事件 Ω， 不可能事件 $\oslash$ 与任何事件独立
2. 若$A与B$独立，则 $A$与$\overline B$ , $\overline{A}与B$， $\overline{A}与\overline{B}$也独立

第二章 随机变量及其分布

随机变量定义

随机变量：

​ $(\Omega,\mathcal{F},P)$是一个概率空间， $\xi(\omega)$ 是定义在 $\Omega$ 内的一个单值函数，如果对任意实数x，有$\{\omega:\xi(\omega)\le x\}\in \mathcal{F}$ , 则称 $\xi(\omega)$ 为随机变量，记作 $\xi$.

可以看到，$\xi(\omega)$是一个函数，ω为自变量，定义域为 Ω 。

分布函数：

​ 称$F(x)=P{\{\xi(\omega)\le x\}}, -\infty<x<+\infty$ 为随机变量 $\xi(\omega)$ 的分布函数

分布函数性质：

1. $0\le F(x) \le 1$
2. $F(x)$单调不减
3. $F(-\infty)=\lim_{x \to -\infty} F(x)=0$,$F(+\infty)=\lim_{x\to +\infty} F(x)=1$
4. $F(x)$是右连续的

几个公式：

$P\{a<\xi(\omega)\le b\}=F(b)-F(a)$

$P\{\xi(\omega)< b\}=F(b^-)$

$P\{\xi(\omega)= b\}=F(b)-F(b^-)$

$P\{a\le\xi(\omega)< b\}=F(b^-)-F(a^-)$

对于连续型随机变量：$F(b) = F(b^-)$

离散型随机变量

分布函数：$F(x)=\sum_{x_k\le x} P\{X=x_k\}$

分布律：$P\{X=x_i\}=p_i,~~~(i=1,2,3,...,n,...)$

常用离散分布

1. 退化分布 $P\{X=c\}=1$

2. 两点分布 $P\{X=k\}=p^{k}(1-p)^{1-k}~~~(k=0,1)$

3. 均匀分布 $P\{X=x_k\}= \frac{1}{n}~~~~~~(k=1,2,3,...,n)$

4. 二项分布

   若 $X\sim B(n, p)$, 则 $P\{X=k\}=C_n^k p^k(1-p)^{n-k}$

5. 泊松分布

   若 $X\sim P(λ)$， 则 $P\{X=k\}=\frac{\lambda ^k}{k!}e^{-\lambda}$

   【泊松定理】：当n很大，$p_n$很小时且$λ>0$时，可以用泊松分布近似为 二项分布，其中 $\lambda =lim_{n \to \infty} ~np_n$

连续型随机变量

分布函数与概率密度关系

$F(x)=\int_{-\infty}^{x}p(x)dx$, 其中 $p(x)$为概率密度函数

常用连续分布

1. 均匀分布 $p(x)=\begin{cases}\frac{1}{b-a} & a\le x\le b \\0& 其它 \end{cases}$

2. 正态分布

   $$p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, -\infty<x<+\infty$$

   正态分布标准化：$Y=\frac{X-\mu}{\sigma}$

3. 指数分布 $p(x)=\begin{cases}\lambda e^{-\lambda x} & x\ge0 \\0& 其它 \end{cases}$，服从指数分布记作 $X\sim Exp(λ)$

   特点：具有无记忆性

正态分布积分常用的公式：

$$\int_{-\infty}^{+\infty} e^{-\frac{t^2}{2}} dt=\sqrt{2\pi}$$

多维随机变量及其分布

由n个随机变量 $X_1, X_2~, ..., X_n~$ 构成的向量 $X=(X_1~, X_2~, ..., X_n~)$称为$n$维随机变量

分布函数：

$$F(x_1, x_2,...,x_n)=P\{X_1\le x_1;X_2\le x_2;...;X_n\le x_n\}$$

二维随机变量

对于n=2时，有下面性质

1. $0\le F(x,y)\le 1$

2. $F(x,y)$关于x和关于y分别是单调非降函数

3. 记住下面公式

   $$\lim_{x \to -\infty}F(x,y)=F(-\infty,y)=0\\ \lim_{y \to \infty} F(x,y)=F(x, -\infty)=0\\ F(+\infty,+\infty)=1$$

4. $F(x,y)$关于每个变元是右连续的

二维离散型随机变量(X,Y)的分布律：

$$P\{X=x_i;Y=y_i\}=p_{ij}~~~~~~(i,j=1,2,3,...,n)$$

二维连续型随机变量(X, Y)的二元分布函数F(x,y)如下：

$$F(x,y)=\int_{-\infty}^x\int_{-\infty}^yp(x,y)dxdy$$

其中$p(x,y)$为联合密度函数

$p(x,y)$性质：

1. 非负性：$p(x,y)\ge0$

2. $\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}p(x,y)dxdy=1$

3. 若$p(x,y)$在$(x,y)$处连续：

   $$\frac{\partial ^2F}{\partial x \partial y}=p(x,y)$$

4. 若D为$xOy$平面的任一区域，则

   $$P\{(X,Y)\in D\}=\iint\limits_{D} p(u,v)dudv$$

边缘分布

分布函数

$F_X(x)=P\{X\le x\}=P\{X\le x;Y<+\infty\}=F(x,+\infty)$

$F_Y(y)=P\{Y\le y\}=P\{X<+\infty;~Y\le y\}=F(+\infty,y)$

分布律

若为离散型，则

$$p_{i\cdot } = \sum_{j}p_{ij} \\ p_{\cdot j} = \sum_{i} p_{ij}$$

若为连续型，则

$$p_X(x)=\int_{-\infty}^{+\infty}p(x,y)dy\\ p_Y(y)=\int_{-\infty}^{+\infty}p(x,y)dx$$

随机变量独立性

连续型：$p(x,y)=p_X(x)p_Y(y)\Longleftrightarrow X,Y独立$

离散型：$p_{ij}=p_{i\cdot}\times p_{\cdot j}\Longleftrightarrow X,Y独立$

条件分布

离散型：

$P\{X=x_i| Y=y_j\}=\frac{p_{ij}}{p_{\cdot j}}\\P\{Y=y_j|X=x_i\}=\frac{p_{ij}}{p_{i\cdot}}$

连续型：

$p(x|y)=\frac{p(x,y)}{p_Y(y)}$

随机变量的函数及其分布

问题: 若$Y=f(X)$，如何根据X的分布推导Y的分布？

单个随机变量

设$Y=f(X)$, 已知映射关系$f$ (如$Y=X^2)$ 以及 随机变量 X 的分布律，求Y的分布？

解：先求 $F_Y(y)=P\{Y\le y\}$ 再求导得 $p_Y(y)=\frac{dF_Y(y)}{dy}$

两个随机变量

若 $Z=f(X,Y)$ ，则 $P\{Z=z_k\}=\sum_{f(x_i,y_i)=z_k}P\{X=x_i;Y=y_i\}$

一般法：

1. 先求$F_Z(z)=P\{Z\le z\}=P\{f(X,Y)\le z\}=\iint\limits_{f(x,y)\le z}p(x,y)dxdy$
2. 对 $F_Z(z)$求导得 $f_Z(z)=\frac{dF_Z}{dz}$

特殊法：

​ 对于 $Z=X+Y, Z=XY, Z=X/Y$几种情况，其概率密度函数可以用下面方式计算：

​ 写出 $Z=g(X, Y)$的形式（如$Z=X+Y$）, 则解出$Y=h(X, Z)$ （如$Y=Z-X$），于是$f_z(z)=\int_{-\infty}^{+\infty}f[x,h(x,z)]\times|\frac{\partial h}{\partial z}|dx$

第三章 随机变量数字特征

数学期望

离散随机变量： $E(X)=\sum_{n=1}^{\infty}x_np_n$

连续随机变量： $E(X)=\int_{-\infty}^{+\infty}xp(x)dx$

注意：有时为了方便，$E(X)$也写作$EX$

随机变量函数Y=f(X)的数学期望E(Y)：

• 离散：$E(Y)=E[f(X)]=\sum_{i=1}^{\infty}f(x_i)p_i$

• 连续：$E(Y)=E[f(X)]=\int_{-\infty}^{+\infty}f(x)p(x)dx$

二维随机变量$Z=f(X,Y)$，若$E(Z)$存在，求$E(Z)$

• 离散：$E(Z)=\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}f(x_i,y_j)p_{ij}$

• 连续：$E(Z)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)p(x,y)dxdy$

数学期望性质

1. $E(C)=C$, ($C$为常数)
2. $E(kX)=kE(X), E(X+Y)=E(X)+E(Y)$ （不需要X、Y独立）
3. $若X、Y独立，E(XY)=E(X)E(Y)$ （注意，不能用该方法证明X、Y是独立的）

方差和矩

方差定义：$D(X)=E[X-E(X)]^2$，标准差 $\sigma_X=\sqrt{D(X)}$

计算公式

方法一（定义法）

• 离散场合：${\color{black} D(X)=E[X-E(X)]^2=\sum_{i=1}^{\infty}(x_i-E(X))^2p_i}$
• 连续场合：${\color{black}D(X)=E[X-E(X)]^2=\int_{-\infty}^{+\infty}(x-E(X))^2p(x)dx}$

方法二

$D(X)=E(X^2)-[E(X)]^2$

方差性质

1. $D(C)=0$, $C$为常数
2. $D(kX)=k^2D(X)$
3. 若X，Y独立，$D(X±Y) = D(X) + D(Y)$

常用分布的期望和方差

对于[正态分布]，有 $E(X^2)=\mu^2+\sigma^2$

其它分布 $E(X^2)=D(X)+[E(X)]^2$

矩

原点矩：k阶原点矩 $\alpha_k=E(X^k)$, $k=1$时即为数学期望E(X)

中心距：k阶中心距 $\mu_k=E[X-E(X)]^k$ , $k=2$时即为方差D(X)

协方差与相关系数

协方差

随机变量X与Y的协方差记为 $cov(X,Y)$，即

$$cov(X,Y)=E[(X-EX)(Y-EY)]$$

协方差性质：

1. $cov(X,Y)=cov(Y,X)$
2. $cov(X,Y)=E(XY)-E(X)E(Y)$
3. $cov(aX, bY)=ab\times cov(X,Y)$
4. $cov(X_1+X_2,Y)=cov(X_1,Y)+cov(X_2,Y)$
5. 若$X，Y$独立，则 $cov(X,Y)=0$
6. $D(X\pm Y)=D(X)+D(Y)\pm 2cov(X,Y)$

相关系数

$$\rho_{XY}=\frac{cov(X,Y)}{\sigma_X\sigma_Y}$$

其中$\sigma_X,\sigma_Y$ 分别为 X，Y的标准差；当 $\rho_{XY}=0$时，则称 X，Y 不相关

性质：

1. 对于任意随机变量X和Y，均有 $|\rho_{XY}|\le1$
2. $\rho_{XY}=1\Longleftrightarrow P\{Y=aX+b\}=1$，其中a和b均为常数且$a\ne0$
3. X和Y相互独立$\rightarrow$ X和Y不相关 （反之不成立，除非X、Y均服从正态分布）

第四章 极限定理

大数定律

大数定律：设$\{X_n\}$是一个随机变量序列，$\{a_n\}$是一个常数序列，若对任意实数ε>0, 都有

$$\lim_{n\to+\infty}P\{\mid\frac{1}{n}\sum_{i=1}^{n}X_i - a_n\mid<\varepsilon \}=1~~即 \frac{1}{n}\sum_{i=1}^{n}X_i-a_n\overset{P}{\rightarrow}0$$

则称$\{X_n\}$服从大数定律。

切比雪夫大数定律：

$$\lim_{n \to \infty} P\{|\frac{1}{n}\sum _{i=1}^{n}X_i-\frac{1}{n}\sum_{i=1}^{n}E(X_i)|<\varepsilon \}=1\\ 即~~~~~ \frac{1}{n}\sum _{i=1}^{n} (X_i-E(X_i))\overset{P}{\rightarrow}0$$

切比雪夫不等式：

$$P\{|X-E(X)|\ge \varepsilon \}\le\frac{D(X)}{\varepsilon ^2}$$

伯努利大数定律：设$n_A$为n重伯努律试验中A出现的次数，p为每次试验中A出现的概率，则对任意实数$ε>0$，都有

$$\lim_{n \to \infty} P\{|\frac{n_A}{n}-p |<\varepsilon \}=1$$

可以理解为，当试验次数n足够大时，A事件发生的频率 $\frac{n_A}{n}$ 近似等于A事件发生的概率

辛钦大数定律：设随机变量序列$\{X_n\}$独立同分布，且$E(X_i)=μ$，则对任意实数$ε>0$，都有

$$\lim_{n \to \infty} P\{|\frac{1}{n}\sum_{i=1}^{n}X_i-\mu |<\varepsilon \}=1$$

中心极限定理

林德贝格-列维中心极限定理（独立同分布中心极限定理）：

​ 设随机变量序列$\{X_n\}$独立同分布，且存在数学期望$E(X_i)=\mu$和方差$D(X_i)=\sigma^2>0$,则对于任意$x$，有

$$\lim_{n \to \infty} P\{\frac{\sum_{i=1}^{n} X_i-n\mu}{\sqrt{n}\sigma } \le x \}=\Phi(x)$$

• 其中 $\Phi (x)=\int_{-\infty }^{+\infty } \frac{1}{\sqrt{2\pi} }e^{\frac{x^2}{2}}dx$ 为标准正态分布函数

• 注意观察，可以发现 $n\mu$就是 $\sum_{i=1}^{n}X_i$的数学期望，分母 $\sqrt{n}\sigma$就是$\sum_{i=1}^{n}X_i$的标准差（可以与下一个定理进行比较，方便记住公式）

该定理表明，独立同分布序列，只要方差存在且不为0，当n足够大，就有

$$\frac{\sum_{i=1}^{n} X_i-n\mu}{\sqrt{n}\sigma } \sim AN(0,1)$$

$AN(0,1)$表示近似(almost)标准正态分布, 从而

$$\sum_{n}^{i=1}X_i\sim AN(n\mu, n\sigma^2)$$

棣莫弗-拉普拉斯定理：设随机变量 $Y_n$ ~ $B(n, p)（n=1,2,...）$，对任意$x$，有

$$\lim_{n \to \infty} P\{\frac{Y_n-np}{\sqrt{np(1-p)} }\le x \}=\Phi(x)$$

（注意与上一个定理——独立同分布中心极限定理，进行对比，方便记忆）

第五章 数理统计基本概念与抽样分布

基本概念

• 总体：在数理统计中，一个随机变量X或分布函数$F(x)$称为一个总体

• 样本：在一个总体$X$中，随机抽取n个个体$X_1,...,X_n$，称为来自总体X的容量为n的样本，通常记为$(X_1,...,X_n)$

• 样本值：在一次抽样观察后，得到的一组数值$(X_1,...,X_n)$，称之为样本$(X_1,...,X_n)$的观测值，简称为样本值

• 样本空间：样本$(X_1,...,X_n)$所有可能取值的全体称为样本空间，记作 $Ω$

随机抽取的样本应该满足以下两个条件，满足这2个条件的称之为简单随机样本

1. 代表性
2. 独立性

样本的分布

设$(X_1,...,X_n)$是来自总体X的一个样本

1. （X是连续情况）若总体X的分布密度函数为$p(x)$，则样本的联合分布密度函数为 $\prod_{i=1}^{n}p(x_i)$
2. （X是离散情况）总体X的分布律为 $P\{X=x_i^*\}=p(x_i^*)$，则样本的联合分布律为 $\prod_{i=1}^{n}p(x_i)$
3. 总体X的分布函数为F(x)，则样本的联合分布函数为 $\prod_{i=1}^{n}F(x_i)$

统计量

定义：

• 设$(X_1,...,X_n)$是来自总体X的一个样本，若样本的函数$f(X_1,X_2,...,X_n)$不含任何未知参数，则称$f(X_1,X_2,...,X_n)$是一个统计量；

• 若$(x_1,x_2,...,x_n)$是一个样本值，则称$f(x_1,x_2,...,x_n)$为统计量$f(X_1,X_2,...,X_n)$ 的一个观测值

可以看到，统计量来自总体（是总体的一个样本），不含任何未知参数，完全由样本来确定，也就是说，根据样本可以求出我们需要的任何一个统计量的值。

例如：设样本$(X_1,...,X_n)$来自正态总体$X$~$N(μ,σ^2)$，其中$μ$已知而$σ$未知，则

1. $\sum_{i=1}^n X_i$ 和 $\frac{1}{n}\sum_{i=1}^{n}(X_i-\mu)^2$ 是统计量
2. $\frac{1}{\sigma^2}\sum_{i=1}^{n}(X_i-\mu)^2$ 不是统计量

常用统计量——样本矩

1. 样本均值 $\overline{X}=\frac{1}{n} \sum_{i=1}^{n}X_i$

2. 样本方差 $S_n^2=\frac{1}{n}\sum_{i=1}^{n}(X_i-\overline{X})^2=\frac{1}{n}\sum_{i=1}^{n}X_i^2-\overline{X}^2$

   样本标准差 $S_n=\sqrt{S_n^2}$

3. 修正样本方差 $S_n^{*^2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline{X})^2=\frac{n}{n-1}S_n^2$

   修正样本标准差 $S_n^{*}=\sqrt{S_n^{*^2}}$

4. 样本k阶原点矩 $A_k=\frac{1}{n} \sum_{i=1}^{n}X_i^k$

5. 样本k阶中心矩 $B_k=\frac{1}{n} \sum_{i=1}^{n}(X_i-\overline{X} )^k$

性质(重要)

1. $E(\overline{X})=E(X)$
2. $D(\overline{X})=\frac{1}{n}D(X)$
3. $E(S_n^2)=\frac{n-1}{n}D(X)$
4. $E(S_n^{*2})=D(X)$

次序统计量（不重要，跳过）

常用统计分布

$\chi$ 分布

定义：设随机变量$X_1,X_2,...,X_n$ 独立同分布，且每个 $X_i \sim N(0,1),~~i=1,2,...,n$,则称随机变量：

$$\chi^2_{n}=\sum_{i=1}^{n}X_i^2$$

服从自由度为n的卡方($\chi^2$)分布, 记为 $\chi^2_n \sim \chi^2(n)$,随机变量 $\chi_n^2$亦被称为 $\chi^2$变量

伽马函数(不需要记)

$$\Gamma(\alpha)=\int_0^{+\infty}x^{\alpha-1}e^{-x}dx , (\alpha>0)$$

根据定义得出以下结论

1. 若总体$X\sim N(0,1),~~(X_1,X_2,...,X_3)$是其中一个样本，则统计量 $\sum_{i=1}^nX_i^2\sim \chi^2(n)$
2. 若总体$X\sim N(\mu,\sigma^2),~~(X_1,X_2,...,X_3)$是其中一个样本，则统计量 $\frac{1}{\sigma^2}\sum_{i=1}^n(X_i-\mu)^2 \sim \chi^2(n)$

性质一

$$E(\chi^2_n)=n \\ D(\chi^2_n)=2n$$

性质二（可加性）

若$X_1\sim \chi^2(n_1), X_2\sim \chi^2(n_2)$, 且 $X_1, X_2$相互独立，则

$$X_1+X_2 \sim \chi^2(n_1+n_2)$$

性质三

$$\chi^2_n\sim AN(n,2n)$$

t 分布

定义：设$X\sim N(0,1), Y\sim \chi^2(n)$, 且$X,Y$相互独立，则称随机变量

$$T=\frac{X}{\sqrt{Y/n}}$$

服从自由度为n的t分布，记为$T\sim t(n)$,随机变量T也称为t变量

t分布是关于y轴对称的

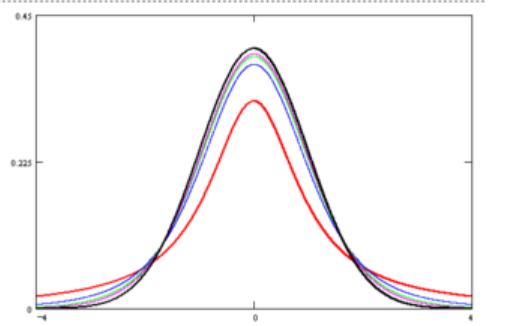
当n=1时，$p(x)=\frac{1}{\pi}\frac{1}{1+x^2}$, 为柯西分布

当n充分大时，t分布趋于标准正态分布

性质一

$$E(T)=0\\ D(T)=\frac{n}{n-2}$$

性质二

$$\lim_{n\to \infty}p(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$$

即n足够大(n>30即可)时，近似看作服从标准正态分布，记作$T\sim AN(0,1)$

但在n较小时，就与标准正态分布有较大差距，在t分布的尾部比标准正态分布的尾部有更大的概率，即

$$P\{|T|\ge t_0\} \ge P\{|X|\ge t_0\}$$

F 分布

定义：设 $X\sim \chi^2(n_1),Y\sim \chi^2(n_2)$, 且X与Y相互独立，则称随机变量 $F=\frac{X/n_1}{Y/n_2}$服从自由度为$(n_1,n_2)$的F分布，记为$F\sim F(n_1,n_2)$，其中$n_1$称为第一自由度，$n_2$称为第二自由度。

性质一，设 $F\sim F(n_1,n_2)$, 则

$$\frac{1}{F} \sim F(n_2,n_1)$$

性质二，设 $T\sim t(n)$, 则

$$T^2\sim F(1,n)$$

概率分布的分位数

定义：设总体X和给定的 $\alpha(0<\alpha<1)$,若存在 $x_{\alpha}$，使得

$$P\{X>x_{\alpha}\}=\alpha$$

则称$x_{\alpha}$为此概率分布的上α分位点(或称临界值)，称$x_{\frac{1}{2}}$为此概率分布的中位数。

标准正态分布的α分位点

$\Phi(u_\alpha)=1-\alpha$

根据标准正态分布的y轴对称性：$u_\alpha=-u_{1-\alpha}$

$\chi^2$分布的α分位点

定义：$P\{\chi^2_n>\chi_\alpha^2(n)\}=\alpha$

t分布的α分位点

定义：$P\{T>t_\alpha(n)\}=\alpha$

根据t分布的y轴对称性，有 $t_\alpha(n)=-t_{1-\alpha}(n)$

当n较大时，有 $t_\alpha=u_\alpha$

F分布的α分位点

定义：$P\{F>F_\alpha(n_1,n_2)\}=\alpha$

性质:

$$F_\alpha(n_1,n_2)= \frac{1}{F_{1-\alpha}(n_2,n_1)}$$

抽样分布(重要)

定理5.3

设总体$X\sim N(\mu,\sigma^2),(X_1,X_2,...,X_n)$是来自总体X的一个样本，则有：

1. $\overline{X}\sim N(\mu, \frac{\sigma^2}{n})$或 $\frac{\overline{X}-\mu}{\sigma /\sqrt{n}}\sim N(0,1)$
2. $\overline{X}$与$S_n^{*2}、S_n^2$相互独立
3. $\frac{(n-1)S_n^{*2}}{\sigma^2}\sim \chi^2(n-1)$或$\frac{nS_n^{2}}{\sigma^2}\sim \chi^2(n-1)$
4. $\frac{\overline{X}-\mu}{S_n^*/\sqrt{n}}\sim t(n-1)$或 $\frac{\overline{X}-\mu}{S_n/\sqrt{n-1}}\sim t(n-1)$

定理5.4

设 $X_1,X_2,\dots,X_{n_{1}}$和$Y_1,Y_2,\dots,Y_{n_2}$分别是来自正态总体 $N(\mu_1, \sigma^2_1)$和$N(\mu_2, \sigma_2^2)$的样本，且这两个样本相互独立，设 $\overline{X},\overline{Y}$分别是两个样本的均值，且 $S_{n_1}^{*^2}, S_{n_2}^{*^2}$分别是这两个样本的修正样本方差，则有：

1. $\frac{S_{n_1}^{*2}/S_{n_2}^{*2}}{\sigma_1^2/\sigma_2^2}\sim F(n_1-1,n_2-1)$
2. 当$\sigma_1^2=\sigma_2^2=\sigma^2$时，有

$$\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{S_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \sim t(n_1+n_2-2)$$

其中

$$S_w=\frac{(n_1-1)S_{n_1}^{*^2}+(n_2-1)S_{n_2}^{*^2}}{n_1+n_2-2}$$

第六章 参数估计

参数的点估计

矩估计法

由样本矩的性质知， 样本矩依概率收敛于相应的样本总体，即

$$A_k=\frac{1}{n}\sum_{i=1}^{n}X_i^k\xrightarrow{P}E(X^k)$$

$$B_k=\frac{1}{n}\sum_{i=1}^{n}(X_i-\overline{X})^k\xrightarrow{P}E(X-EX)^k$$

矩估计的基本思想是利用样本矩来估计总体矩获得参数的估计量（因为样本足够大时，样本矩与总体矩之间的差距可任意小），基本步骤如下：

1. 计算【总体X】从1阶矩到m阶矩（m为未知参数的个数）：$E(X), E(X^2),\dots,E(X^m)$
2. 计算【样本】的矩：$A_1, A_2,\dots,A_m$
3. 解方程组

$$\begin{cases} A_1=E(X)\\ A_2=E(X^2)\\ \cdots \\ A_m=E(X^m) \end{cases}$$

得到未知参数$~{\theta}_i~$的估计值

$$\begin{cases} \hat{\theta}_1=\hat{\theta}_1(X_1,X_2,\dots,X_n) \\ \hat{\theta}_2=\hat{\theta}_2(X_1,X_2,\dots,X_n) \\ \cdots \\ \hat{\theta}_m=\hat{\theta}_m(X_1,X_2,\dots,X_n) \end{cases}$$

注意：对于样本来说，样本的所有参量认为是已知的，而总体的参量是我们需要估计的，因此，根据样本依概率矩收敛于总体矩的特性知：可以通过样本来估计总体的参量。

例如：样本的均值$\overline{X}$和方差$S_n^2$总是总体的数学期望$E(X)$和方差$D(X)$的矩估计量。

最大似然估计法

前提：总体的分布形式已知，如已知$p(x;\theta),\theta$为未知参数

似然函数：样本的联合分布律 $L(\theta)=\prod_{i=1}^{n}p(x_i;\theta)$

基本思想：在试验中概率最大(即$L(\theta)最大$)的事件最有可能出现，我们就是要找到这样一个参数 θ 使得其发生的概率最大。

求解步骤：

1. 求似然函数：$L(\theta)=\prod_{i=1}^{n}p(x_i;\theta)$
2. 求$L(\theta)$最大值，一般通过求导使得 $\frac{\partial \ln L(\theta)}{\partial \theta}\mid_{\theta={\hat{\theta}}}=0$(该方程称为似然方程), 有多个参数就分别对该参数求偏导
3. 求解第二步的方程，得到参数的估计值$\theta_i=\hat{\theta_i}$

注意：若无法通过求导方式求解似然函数$L(θ)$最大值，可以通过分析$L(θ)$单调特性，以及$\theta$可能取值范围，从 θ取值范围中选择一个值使得$L(θ)$取得最大值，最后用该值作为该参数的估计值

估计量的优良性评判

既然是估计量，那与真实值之间就存在误差，因此需要判断估计量是否满足我们的要求，可以通过下面的几个准则来进行评判。

无偏性

定义：设$(X_1,X_2,\dots,X_n)$是来自总体$X$的一个样本，$\theta \in \Theta$ 为总体分布中的未知参数，$\hat{\theta}=\hat{\theta}(X_1,X_2,\dots,X_n)$ 是 $θ$ 的一个估计量，若对任意 $\theta \in \Theta$，有

$$E(\hat{\theta})=\theta$$

则 $\hat{\theta}$ 为 $θ$ 的无偏估计(量).