第一章 随机事件及其概率
样本点:对于随机试验,把每一个可能的结果称为样本点
随机事件:某些样本点的集合
基本事件:单个样本点构成的集合
样本空间(或必然事件):所有样本点构成的集合,记作 Ω
不可能事件:不含任何样本点,记作 ⊘
事件关系运算
交换律:A∪B=B∪A, A∩B=B∩A
结合律:A∪(B∪C)=(A∪B)∪C, A(BC)=(AB)C
分配律:A(B∪C)=(AB)∪(AC), (AB)∪C=(A∪C)(B∪C), A(B−C)=AB−AC
对偶率:A∪B=A∩B, A∩B=A∪B
事件的积:A∩B=AB
事件的和:A∪BAB互不相容直和A+B
事件的差:A−B=AΩ−AB=AB
概率性质
-
对于任意事件A,0≤P(A)≤1
-
P(Ω)=1,P(⊘)=0
-
对于两两互斥的有限多个事件A1 ,A2 ,...,Am
P(A1 +A2 +...+Am )=P(A1 )+P(A2 )+...+P(Am )
推论
-
P(A)=1−P(A)
-
任意时候:P(A−B)=P(A)−P(AB)
若 A⊃B , 则 P(A−B)=P(A)−P(B)
-
P(A∪B)=P(A)+P(B)−P(AB)
因此,P(AB)=P(A)+P(B)−P(A∪B)
条件概率 全概率公式 Bayes公式
条件概率
P(A∣B)=P(B)P(AB)
乘法定理 P(AB)=P(B)P(A∣B)=P(A)P(B∣A)
全概率公式
P(B)=i=1∑nP(AiB)=i=1∑nP(Ai)P(B∣Ai)
Bayes公式
P(Ai∣B)=P(B)P(AiB)=∑i=1nP(Ai)P(B∣Ai)P(Ai)P(B∣Ai)
事件的独立性
定义:若 P(AB)=P(A)P(B), 则A与B是相互独立的
性质:
- 必然事件 Ω, 不可能事件 ⊘ 与任何事件独立
- 若A与B独立,则 A与B , A与B, A与B也独立
第二章 随机变量及其分布
随机变量定义
随机变量:
(Ω,F,P)是一个概率空间, ξ(ω) 是定义在 Ω 内的一个单值函数,如果对任意实数x,有{ω:ξ(ω)≤x}∈F , 则称 ξ(ω) 为随机变量,记作 ξ.
可以看到,ξ(ω)是一个函数,ω为自变量,定义域为 Ω 。
分布函数:
称F(x)=P{ξ(ω)≤x},−∞<x<+∞ 为随机变量 ξ(ω) 的分布函数
分布函数性质:
- 0≤F(x)≤1
- F(x)单调不减
- F(−∞)=limx→−∞F(x)=0,F(+∞)=limx→+∞F(x)=1
- F(x)是右连续的
几个公式:
P{a<ξ(ω)≤b}=F(b)−F(a)
P{ξ(ω)<b}=F(b−)
P{ξ(ω)=b}=F(b)−F(b−)
P{a≤ξ(ω)<b}=F(b−)−F(a−)
对于连续型随机变量:F(b)=F(b−)
离散型随机变量
分布函数:F(x)=∑xk≤xP{X=xk}
分布律:P{X=xi}=pi, (i=1,2,3,...,n,...)
| X |
x1 |
x2 |
x3 |
… |
| pi |
p1 |
p2 |
p3 |
… |
常用离散分布
-
退化分布 P{X=c}=1
-
两点分布 P{X=k}=pk(1−p)1−k (k=0,1)
-
均匀分布 P{X=xk}=n1 (k=1,2,3,...,n)
-
二项分布
若 X∼B(n,p), 则 P{X=k}=Cnkpk(1−p)n−k
-
泊松分布
若 X∼P(λ), 则 P{X=k}=k!λke−λ
【泊松定理】:当n很大,pn很小时且λ>0时,可以用泊松分布近似为 二项分布,其中 λ=limn→∞ npn
连续型随机变量
分布函数与概率密度关系
F(x)=∫−∞xp(x)dx, 其中 p(x)为概率密度函数
常用连续分布
-
均匀分布 p(x)={b−a10a≤x≤b其它
-
正态分布
p(x)=2πσ1e−2σ2(x−μ)2,−∞<x<+∞
正态分布标准化:Y=σX−μ
-
指数分布 p(x)={λe−λx0x≥0其它,服从指数分布记作 X∼Exp(λ)
特点:具有无记忆性
正态分布积分常用的公式:
∫−∞+∞e−2t2dt=2π
多维随机变量及其分布
由n个随机变量 X1,X2 ,...,Xn 构成的向量 X=(X1 ,X2 ,...,Xn )称为n维随机变量
分布函数:
F(x1,x2,...,xn)=P{X1≤x1;X2≤x2;...;Xn≤xn}
二维随机变量
对于n=2时,有下面性质
-
0≤F(x,y)≤1
-
F(x,y)关于x和关于y分别是单调非降函数
-
记住下面公式
x→−∞limF(x,y)=F(−∞,y)=0y→∞limF(x,y)=F(x,−∞)=0F(+∞,+∞)=1
-
F(x,y)关于每个变元是右连续的
二维离散型随机变量(X,Y)的分布律:
P{X=xi;Y=yi}=pij (i,j=1,2,3,...,n)
二维连续型随机变量(X, Y)的二元分布函数F(x,y)如下:
F(x,y)=∫−∞x∫−∞yp(x,y)dxdy
其中p(x,y)为联合密度函数
p(x,y)性质:
-
非负性:p(x,y)≥0
-
∫−∞+∞∫−∞+∞p(x,y)dxdy=1
-
若p(x,y)在(x,y)处连续:
∂x∂y∂2F=p(x,y)
-
若D为xOy平面的任一区域,则
P{(X,Y)∈D}=D∬p(u,v)dudv
边缘分布
分布函数
FX(x)=P{X≤x}=P{X≤x;Y<+∞}=F(x,+∞)
FY(y)=P{Y≤y}=P{X<+∞; Y≤y}=F(+∞,y)
分布律
若为离散型,则
pi⋅=j∑pijp⋅j=i∑pij
若为连续型,则
pX(x)=∫−∞+∞p(x,y)dypY(y)=∫−∞+∞p(x,y)dx
随机变量独立性
连续型:p(x,y)=pX(x)pY(y)⟺X,Y独立
离散型:pij=pi⋅×p⋅j⟺X,Y独立
条件分布
离散型:
P{X=xi∣Y=yj}=p⋅jpijP{Y=yj∣X=xi}=pi⋅pij
连续型:
p(x∣y)=pY(y)p(x,y)
随机变量的函数及其分布
问题: 若Y=f(X),如何根据X的分布推导Y的分布?
单个随机变量
设Y=f(X), 已知映射关系f (如Y=X2) 以及 随机变量 X 的分布律,求Y的分布?
解:先求 FY(y)=P{Y≤y} 再求导得 pY(y)=dydFY(y)
两个随机变量
若 Z=f(X,Y) ,则 P{Z=zk}=∑f(xi,yi)=zkP{X=xi;Y=yi}
一般法:
- 先求FZ(z)=P{Z≤z}=P{f(X,Y)≤z}=f(x,y)≤z∬p(x,y)dxdy
- 对 FZ(z)求导得 fZ(z)=dzdFZ
特殊法:
对于 Z=X+Y,Z=XY,Z=X/Y几种情况,其概率密度函数可以用下面方式计算:
写出 Z=g(X,Y)的形式(如Z=X+Y), 则解出Y=h(X,Z) (如Y=Z−X),于是fz(z)=∫−∞+∞f[x,h(x,z)]×∣∂z∂h∣dx
第三章 随机变量数字特征
数学期望
离散随机变量: E(X)=∑n=1∞xnpn
连续随机变量: E(X)=∫−∞+∞xp(x)dx
注意:有时为了方便,E(X)也写作EX
随机变量函数Y=f(X)的数学期望E(Y):
-
离散:E(Y)=E[f(X)]=∑i=1∞f(xi)pi
-
连续:E(Y)=E[f(X)]=∫−∞+∞f(x)p(x)dx
二维随机变量Z=f(X,Y),若E(Z)存在,求E(Z)
-
离散:E(Z)=∑i=1∞∑j=1∞f(xi,yj)pij
-
连续:E(Z)=∫−∞+∞∫−∞+∞f(x,y)p(x,y)dxdy
数学期望性质
- E(C)=C, (C为常数)
- E(kX)=kE(X),E(X+Y)=E(X)+E(Y) (不需要X、Y独立)
- 若X、Y独立,E(XY)=E(X)E(Y) (注意,不能用该方法证明X、Y是独立的)
方差和矩
方差定义:D(X)=E[X−E(X)]2,标准差 σX=D(X)
计算公式
方法一(定义法)
- 离散场合:D(X)=E[X−E(X)]2=∑i=1∞(xi−E(X))2pi
- 连续场合:D(X)=E[X−E(X)]2=∫−∞+∞(x−E(X))2p(x)dx
方法二
D(X)=E(X2)−[E(X)]2
方差性质
- D(C)=0, C为常数
- D(kX)=k2D(X)
- 若X,Y独立,D(X±Y)=D(X)+D(Y)
常用分布的期望和方差
| 分布 |
期望E(X) |
方差D(X) |
| 二项分布(离散) |
np |
np(1−p) |
| 泊松分布(离散) |
λ |
λ |
| 几何分布(离散) |
1/p |
(1−p)/p2 |
| 指数分布(连续) |
1/λ |
1/λ2 |
| 均匀分布(连续) |
(a+b)/2 |
(a−b)2/12 |
| 正态分布(连续) |
μ |
σ2 |
对于[正态分布],有 E(X2)=μ2+σ2
其它分布 E(X2)=D(X)+[E(X)]2
矩
原点矩:k阶原点矩 αk=E(Xk), k=1时即为数学期望E(X)
中心距:k阶中心距 μk=E[X−E(X)]k , k=2时即为方差D(X)
协方差与相关系数
协方差
随机变量X与Y的协方差记为 cov(X,Y),即
cov(X,Y)=E[(X−EX)(Y−EY)]
协方差性质:
- cov(X,Y)=cov(Y,X)
- cov(X,Y)=E(XY)−E(X)E(Y)
- cov(aX,bY)=ab×cov(X,Y)
- cov(X1+X2,Y)=cov(X1,Y)+cov(X2,Y)
- 若X,Y独立,则 cov(X,Y)=0
- D(X±Y)=D(X)+D(Y)±2cov(X,Y)
相关系数
ρXY=σXσYcov(X,Y)
其中σX,σY 分别为 X,Y的标准差;当 ρXY=0时,则称 X,Y 不相关
性质:
- 对于任意随机变量X和Y,均有 ∣ρXY∣≤1
- ρXY=1⟺P{Y=aX+b}=1,其中a和b均为常数且a=0
- X和Y相互独立→ X和Y不相关 (反之不成立,除非X、Y均服从正态分布)
第四章 极限定理
大数定律
大数定律:设{Xn}是一个随机变量序列,{an}是一个常数序列,若对任意实数ε>0, 都有
n→+∞limP{∣n1i=1∑nXi−an∣<ε}=1 即n1i=1∑nXi−an→P0
则称{Xn}服从大数定律。
切比雪夫大数定律:
n→∞limP{∣n1i=1∑nXi−n1i=1∑nE(Xi)∣<ε}=1即 n1i=1∑n(Xi−E(Xi))→P0
切比雪夫不等式:
P{∣X−E(X)∣≥ε}≤ε2D(X)
伯努利大数定律:设nA为n重伯努律试验中A出现的次数,p为每次试验中A出现的概率,则对任意实数ε>0,都有
n→∞limP{∣nnA−p∣<ε}=1
可以理解为,当试验次数n足够大时,A事件发生的频率 nnA 近似等于A事件发生的概率
辛钦大数定律:设随机变量序列{Xn}独立同分布,且E(Xi)=μ,则对任意实数ε>0,都有
n→∞limP{∣n1i=1∑nXi−μ∣<ε}=1
中心极限定理
林德贝格-列维中心极限定理(独立同分布中心极限定理):
设随机变量序列{Xn}独立同分布,且存在数学期望E(Xi)=μ和方差D(Xi)=σ2>0,则对于任意x,有
n→∞limP{nσ∑i=1nXi−nμ≤x}=Φ(x)
-
其中 Φ(x)=∫−∞+∞2π1e2x2dx 为标准正态分布函数
-
注意观察,可以发现 nμ就是 ∑i=1nXi的数学期望,分母 nσ就是∑i=1nXi的标准差(可以与下一个定理进行比较,方便记住公式)
该定理表明,独立同分布序列,只要方差存在且不为0,当n足够大,就有
nσ∑i=1nXi−nμ∼AN(0,1)
AN(0,1)表示近似(almost)标准正态分布, 从而
n∑i=1Xi∼AN(nμ,nσ2)
棣莫弗-拉普拉斯定理:设随机变量 Yn ~ B(n,p)(n=1,2,...),对任意x,有
n→∞limP{np(1−p)Yn−np≤x}=Φ(x)
(注意与上一个定理——独立同分布中心极限定理,进行对比,方便记忆)
第五章 数理统计基本概念与抽样分布
基本概念
-
总体:在数理统计中,一个随机变量X或分布函数F(x)称为一个总体
-
样本:在一个总体X中,随机抽取n个个体X1,...,Xn,称为来自总体X的容量为n的样本,通常记为(X1,...,Xn)
-
样本值:在一次抽样观察后,得到的一组数值(X1,...,Xn),称之为样本(X1,...,Xn)的观测值,简称为样本值
-
样本空间:样本(X1,...,Xn)所有可能取值的全体称为样本空间,记作 Ω
随机抽取的样本应该满足以下两个条件,满足这2个条件的称之为简单随机样本
- 代表性
- 独立性
样本的分布
设(X1,...,Xn)是来自总体X的一个样本
- (X是连续情况)若总体X的分布密度函数为p(x),则样本的联合分布密度函数为 ∏i=1np(xi)
- (X是离散情况)总体X的分布律为 P{X=xi∗}=p(xi∗),则样本的联合分布律为 ∏i=1np(xi)
- 总体X的分布函数为F(x),则样本的联合分布函数为 ∏i=1nF(xi)
统计量
定义:
-
设(X1,...,Xn)是来自总体X的一个样本,若样本的函数f(X1,X2,...,Xn)不含任何未知参数,则称f(X1,X2,...,Xn)是一个统计量;
-
若(x1,x2,...,xn)是一个样本值,则称f(x1,x2,...,xn)为统计量f(X1,X2,...,Xn) 的一个观测值
可以看到,统计量来自总体(是总体的一个样本),不含任何未知参数,完全由样本来确定,也就是说,根据样本可以求出我们需要的任何一个统计量的值。
例如:设样本(X1,...,Xn)来自正态总体X~N(μ,σ2),其中μ已知而σ未知,则
- ∑i=1nXi 和 n1∑i=1n(Xi−μ)2 是统计量
- σ21∑i=1n(Xi−μ)2 不是统计量
常用统计量——样本矩
-
样本均值 X=n1∑i=1nXi
-
样本方差 Sn2=n1∑i=1n(Xi−X)2=n1∑i=1nXi2−X2
样本标准差 Sn=Sn2
-
修正样本方差 Sn∗2=n−11∑i=1n(Xi−X)2=n−1nSn2
修正样本标准差 Sn∗=Sn∗2
-
样本k阶原点矩 Ak=n1∑i=1nXik
-
样本k阶中心矩 Bk=n1∑i=1n(Xi−X)k
性质(重要)
- E(X)=E(X)
- D(X)=n1D(X)
- E(Sn2)=nn−1D(X)
- E(Sn∗2)=D(X)
次序统计量(不重要,跳过)
常用统计分布
χ 分布
定义:设随机变量X1,X2,...,Xn 独立同分布,且每个 Xi∼N(0,1), i=1,2,...,n,则称随机变量:
χn2=i=1∑nXi2
服从自由度为n的卡方(χ2)分布, 记为 χn2∼χ2(n),随机变量 χn2亦被称为 χ2变量
伽马函数(不需要记)
Γ(α)=∫0+∞xα−1e−xdx,(α>0)
根据定义得出以下结论
- 若总体X∼N(0,1), (X1,X2,...,X3)是其中一个样本,则统计量 ∑i=1nXi2∼χ2(n)
- 若总体X∼N(μ,σ2), (X1,X2,...,X3)是其中一个样本,则统计量 σ21∑i=1n(Xi−μ)2∼χ2(n)
性质一
E(χn2)=nD(χn2)=2n
性质二(可加性)
若X1∼χ2(n1),X2∼χ2(n2), 且 X1,X2相互独立,则
X1+X2∼χ2(n1+n2)
性质三
χn2∼AN(n,2n)
t 分布
定义:设X∼N(0,1),Y∼χ2(n), 且X,Y相互独立,则称随机变量
T=Y/nX
服从自由度为n的t分布,记为T∼t(n),随机变量T也称为t变量
t分布是关于y轴对称的
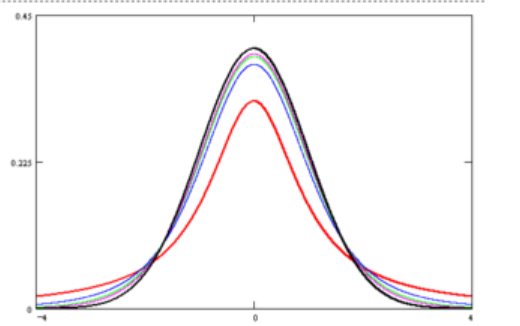
当n=1时,p(x)=π11+x21, 为柯西分布
当n充分大时,t分布趋于标准正态分布
性质一
E(T)=0D(T)=n−2n
性质二
n→∞limp(x)=2π1e−2x2
即n足够大(n>30即可)时,近似看作服从标准正态分布,记作T∼AN(0,1)
但在n较小时,就与标准正态分布有较大差距,在t分布的尾部比标准正态分布的尾部有更大的概率,即
P{∣T∣≥t0}≥P{∣X∣≥t0}
F 分布
定义:设 X∼χ2(n1),Y∼χ2(n2), 且X与Y相互独立,则称随机变量 F=Y/n2X/n1服从自由度为(n1,n2)的F分布,记为F∼F(n1,n2),其中n1称为第一自由度,n2称为第二自由度。
性质一,设 F∼F(n1,n2), 则
F1∼F(n2,n1)
性质二,设 T∼t(n), 则
T2∼F(1,n)
概率分布的分位数
定义:设总体X和给定的 α(0<α<1),若存在 xα,使得
P{X>xα}=α
则称xα为此概率分布的上α分位点(或称临界值),称x21为此概率分布的中位数。

标准正态分布的α分位点
Φ(uα)=1−α
根据标准正态分布的y轴对称性:uα=−u1−α
χ2分布的α分位点
定义:P{χn2>χα2(n)}=α
t分布的α分位点
定义:P{T>tα(n)}=α
根据t分布的y轴对称性,有 tα(n)=−t1−α(n)
当n较大时,有 tα=uα
F分布的α分位点
定义:P{F>Fα(n1,n2)}=α
性质:
Fα(n1,n2)=F1−α(n2,n1)1
抽样分布(重要)
定理5.3
设总体X∼N(μ,σ2),(X1,X2,...,Xn)是来自总体X的一个样本,则有:
- X∼N(μ,nσ2)或 σ/nX−μ∼N(0,1)
- X与Sn∗2、Sn2相互独立
- σ2(n−1)Sn∗2∼χ2(n−1)或σ2nSn2∼χ2(n−1)
- Sn∗/nX−μ∼t(n−1)或 Sn/n−1X−μ∼t(n−1)
定理5.4
设 X1,X2,…,Xn1和Y1,Y2,…,Yn2分别是来自正态总体 N(μ1,σ12)和N(μ2,σ22)的样本,且这两个样本相互独立,设 X,Y分别是两个样本的均值,且 Sn1∗2,Sn2∗2分别是这两个样本的修正样本方差,则有:
- σ12/σ22Sn1∗2/Sn2∗2∼F(n1−1,n2−1)
- 当σ12=σ22=σ2时,有
Swn11+n21(X−Y)−(μ1−μ2)∼t(n1+n2−2)
其中
Sw=n1+n2−2(n1−1)Sn1∗2+(n2−1)Sn2∗2
第六章 参数估计
参数的点估计
矩估计法
由样本矩的性质知, 样本矩依概率收敛于相应的样本总体,即
Ak=n1i=1∑nXikPE(Xk)
Bk=n1i=1∑n(Xi−X)kPE(X−EX)k
矩估计的基本思想是利用样本矩来估计总体矩获得参数的估计量(因为样本足够大时,样本矩与总体矩之间的差距可任意小),基本步骤如下:
- 计算【总体X】从1阶矩到m阶矩(m为未知参数的个数):E(X),E(X2),…,E(Xm)
- 计算【样本】的矩:A1,A2,…,Am
- 解方程组
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧A1=E(X)A2=E(X2)⋯Am=E(Xm)
得到未知参数 θi 的估计值
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧θ^1=θ^1(X1,X2,…,Xn)θ^2=θ^2(X1,X2,…,Xn)⋯θ^m=θ^m(X1,X2,…,Xn)
注意:对于样本来说,样本的所有参量认为是已知的,而总体的参量是我们需要估计的,因此,根据样本依概率矩收敛于总体矩的特性知:可以通过样本来估计总体的参量。
例如:样本的均值X和方差Sn2总是总体的数学期望E(X)和方差D(X)的矩估计量。
最大似然估计法
前提:总体的分布形式已知,如已知p(x;θ),θ为未知参数
似然函数:样本的联合分布律 L(θ)=∏i=1np(xi;θ)
基本思想:在试验中概率最大(即L(θ)最大)的事件最有可能出现,我们就是要找到这样一个参数 θ 使得其发生的概率最大。
求解步骤:
- 求似然函数:L(θ)=∏i=1np(xi;θ)
- 求L(θ)最大值,一般通过求导使得 ∂θ∂lnL(θ)∣θ=θ^=0(该方程称为似然方程), 有多个参数就分别对该参数求偏导
- 求解第二步的方程,得到参数的估计值θi=θi^
注意:若无法通过求导方式求解似然函数L(θ)最大值,可以通过分析L(θ)单调特性,以及θ可能取值范围,从 θ取值范围中选择一个值使得L(θ)取得最大值,最后用该值作为该参数的估计值
估计量的优良性评判
既然是估计量,那与真实值之间就存在误差,因此需要判断估计量是否满足我们的要求,可以通过下面的几个准则来进行评判。
无偏性
定义:设(X1,X2,…,Xn)是来自总体X的一个样本,θ∈Θ 为总体分布中的未知参数,θ^=θ^(X1,X2,…,Xn) 是 θ 的一个估计量,若对任意 θ∈Θ,有
E(θ^)=θ
则 θ^ 为 θ 的无偏估计(量).
-
估计量的偏差:bn=E[θ^(X1,X2,…,Xn)]−θ
-
有偏估计量:当 bn=0 时,称 θ^ 为 θ 的有偏估计(量)
-
渐进无偏估计量:若limn→∞bn=0, 则称 θ^ 为 θ 的渐进无偏估计(量)
有效性
定义:设 θ^1=θ^1(X1,X2,…,Xn) 和 θ^2=θ^2(X1,X2,…,Xn) 均为参数 θ 的无偏估计量,若
D(θ^1)<D(θ^2)
则称 θ^1 比 θ^2 有效
在多个无偏估计量中,方差最小(最有效)那个被称为最小方差无偏估计量
相合性(一致性)
一个优良的估计量,不仅是无偏的,且具有较小的方差,还希望当样本容量n增大时,估计量能在某种意义下收敛于被估计的参数,这就是 相合性(或一致性)
定义:设 θ^n=θ^n(X1,X2,…,Xn)是参数 θ 的估计量,如果当 n 增大时,θ^n 依概率收敛于 θ ,即对任意 ε>0 ,有
n→∞limP{∣θ^n−θ∣<ε}=1或n→∞limP{∣θ^n−θ∣≥ε}=0
则称 θ^n 是 θ 的相合估计(量),或一致估计(量)
定理:设 θ^n=θ^n(X1,X2,…,Xn)是参数 θ 的一个估计量,若
n→∞limE(θ^n)=θ且n→∞limD(θ^n)=0
则 θ^n 是 θ 的相合估计(量),或一致估计(量)
参数的区间估计
定义:设总体X的分布函数为 F(x;θ),θ是未知参数,(X1,X2,…,Xn)是来自总体X的一个样本。对于给定的 α(0<α<1),确定两个统计量 θ^1=θ^1(X1,X2,…,Xn) 和 θ^2=θ^2(X1,X2,…,Xn),使得
P{θ^1<θ<θ^2}=1−α
则称随机区间 (θ^1,θ^2) 为参数 θ 的置信度为 1−α 的置信区间,
- 置信下限:θ^1
- 置信上限:θ^2
- 置信度(置信水平):1−α
如果置信区间只有一边,如:
P{θ^1<θ}=1−α 或 P{θ<θ^2}=1−α
则称置信区间 (θ^1,+∞) 或 (−∞,θ^2) 为单侧置信区间
求置信区间步骤
- 确定统计量 W
- 给定置信度1−α,写出下面的式子
P{a<W<b}, 通常取a=x1−2α,b=x2α
x1−2α 和 x2α 分别为对应分布上的 1−2α 和 2α 分位点。可以看出,给定置信度1−α是用来确定 x1−2α 和 x2α的值的
3. 上面已经求出a, b的值,所以只需要解出下面的不等式即可得出参数区间(θ^1,θ2^)
a<W<b
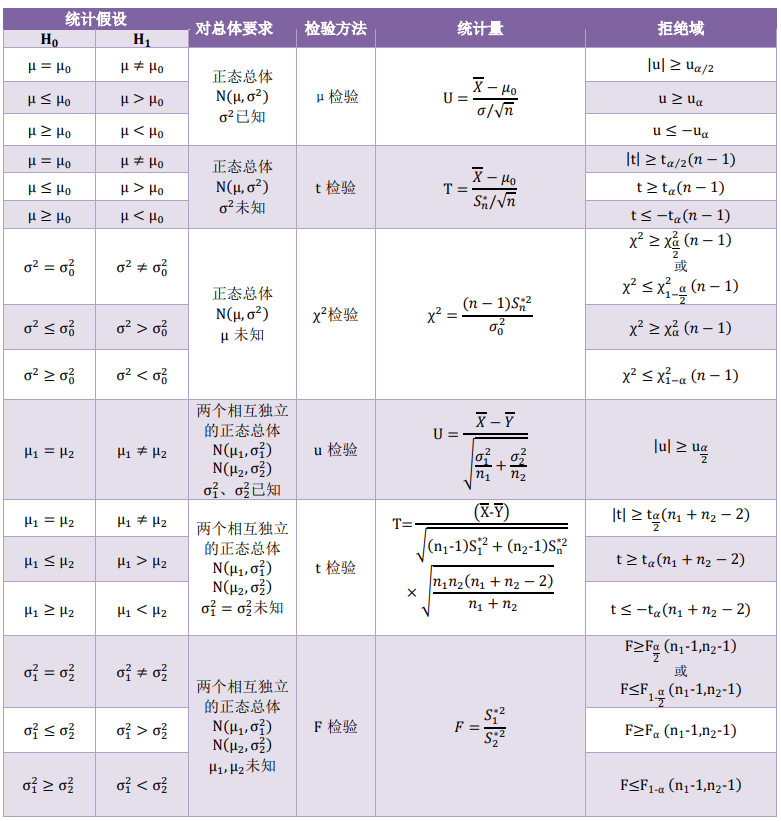
不同分布在不同情况下应取什么统计量,参考下表

第七章 假设检验
基本原理
假设检验的基本原理:给定一个假设H0,为了检验H0是否正确,首先假定H0是正确的,然后根据抽取到的样本来判断是接收还是拒绝该假设。如果样本中出现了不合理的观测值,应该拒绝H0,否则应该接受假设H0
“不合理”指的是小概率事件发生,常用 α 来表示这个小概率,α也被称为检验的显著性水平
拒绝域与临界值
拒绝域 and 接受域:设Ω 是所有样本观测值 x=(x1,x2,…,xn) 的集合,令
W={x∣x∈Ω且使H0不成立}
此集合为 H0的拒绝域,其余集 W 称为 H0 的接受域
从某种意义上说,设计一个检验,本质上就是找到一个恰当的拒绝域W,使得当 H0成立时
P{x∈W∣H0成立}=α
后面我们常把“小概率事件”视为与拒绝域W是等价的
两类错误
第I类错误(弃真错误):假设H0经过检验后是真的,但根据一次抽样结果拒绝了 H0,叫做犯了第I类错误;
第II类错误(纳伪错误):假设H0经过检验后是假的,但根据一次抽样结果接受了 H0,叫做犯了第II类错误。
通常只规定 α 的取值,即控制犯第I类错误的概率,而使犯第二类错误的概率尽可能小,要使两者犯错的概率都小,就必须增大样本容量。
假设检验的基本步骤
- 根据实际问题的要求,提出原假设 H0 和备选假设 H1,通常 H1 与 H0 区间互补(做题时这一步由题目给出)
- 构造统计量 T
- 给定显著性水平 α (题目给出),确定拒绝域
- 计算观察值 t0
- 作出判断:若 t0∈W,则拒绝H0,接受 H1;反之接受 H0,拒绝 H1。
根据不同情形选择不同统计量,参考下表: